La batalla de Austerlitz es reconocida como una de las más brillantes victorias militares de Napoleón Bonaparte. En 1805, este emperador francés, conocido por su astucia estratégica, logró superar a las fuerzas combinadas de Austria y Rusia. Pero, ¿sabías que las matemáticas jugaron un papel crucial en este resultado?
La estrategia de Napoleón: un enfoque matemático
La estrategia de Napoleón en la batalla de Austerlitz no solo fue un ejemplo de maniobra militar envolvente, sino también un caso de uso ingenioso de la matemática en la táctica militar. Napoleón aplicó principios matemáticos para maximizar la eficiencia de sus fuerzas y minimizar su exposición al enemigo.

Se centró en la distribución óptima de sus tropas en el campo de batalla, así como en calcular la mejor ruta de avance y retirada para su ejército. También hizo uso de la geometría y trigonometría para determinar las posiciones más ventajosas en el terreno, tomando en cuenta la topografía y las líneas de visión.
Además, Napoleón también era consciente de la importancia de la sincronización en las operaciones militares. Utilizó cálculos para coordinar los movimientos de sus diferentes unidades y garantizar que sus ataques fueran simultáneos, maximizando así su impacto.
En el caso de Austerlitz, estas tácticas matemáticas permitieron a Napoleón superar a un enemigo numéricamente superior y lograr una de sus más brillantes victorias.
Quién ganó y cuánto duró la batalla de Austerlitz en 1805
La victoria en la batalla de Austerlitz fue para el ejército francés, encabezado por el emperador Napoleón Bonaparte. A pesar de estar en desventaja numérica, con alrededor de 72.000 hombres frente a las fuerzas combinadas austro-rusas de aproximadamente 85.000, Napoleón logró un triunfo aplastante.

En cuanto a la duración, la batalla tuvo lugar el 2 de diciembre de 1805. Aunque no se especifica la duración exacta del enfrentamiento, las batallas de la época napoleónica solían durar entre unas pocas horas y varios días.
La batalla de Austerlitz tuvo lugar en el actual territorio de la República Checa, específicamente en una localidad llamada Austerlitz, ahora conocida como Slavkov u Brna. Aproximadamente a unos 10 km al sureste de Brno, en Moravia, entonces parte del Imperio austriaco.
La ubicación estratégica de la batalla fue un factor crucial en la victoria de Napoleón. La posición elevada de los Altos de Pratzen, por ejemplo, permitió a Napoleón observar y controlar el campo de batalla, asegurando una ventaja táctica clave.
Además, la cuidadosa selección de la ubicación también permitió a Napoleón hacer un uso efectivo de sus tácticas matemáticas, aprovechando la topografía del terreno para maximizar la eficiencia de sus fuerzas.

El uso de las matemáticas en la táctica militar
Para entender cómo Napoleón aplicó las matemáticas en la batalla de Austerlitz, es esencial comprender la situación y las condiciones estratégicas de ese momento. El 2 de diciembre de 1805, el ejército de Napoleón se enfrentó a las fuerzas combinadas ruso-austríacas. A pesar de estar en desventaja numérica, Napoleón tenía una estrategia: engañar al enemigo haciéndole creer que su ejército era débil.
Este plan implicó una serie de cálculos y estimaciones precisas. Napoleón usó la distribución óptima de sus tropas y aplicó principios de geometría y trigonometría para determinar las posiciones más ventajosas en el terreno. Además, utilizó el concepto de sincronización para coordinar los movimientos de sus tropas, asegurando que los ataques fueran simultáneos y más efectivos.
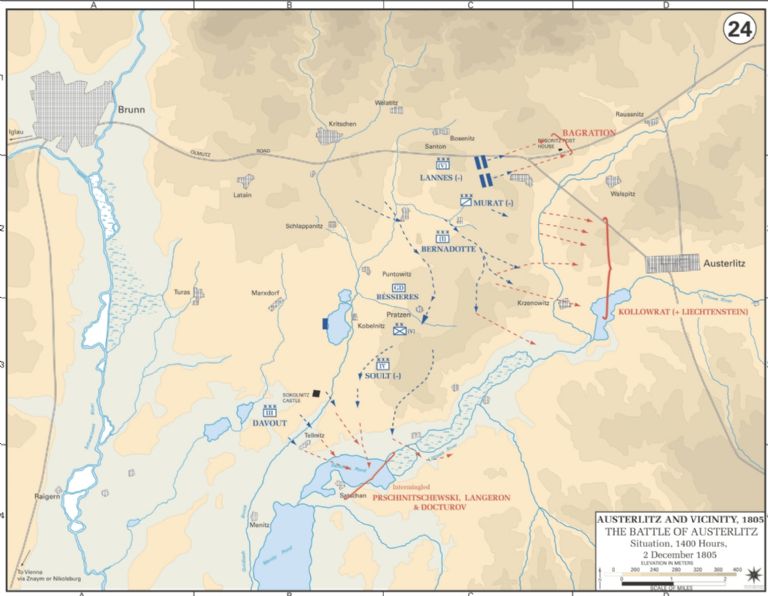
Al analizar la batalla de Austerlitz, podemos observar cómo la aplicación práctica de las matemáticas puede resultar en una victoria militar, incluso cuando las probabilidades parecen estar en contra.
La fórmula matemática usada por Napoleón
El Teorema de Napoleón es una fórmula matemática que se le atribuye a Napoleón Bonaparte, aunque no hay pruebas tangibles de que sea el verdadero autor. Este teorema es un resultado geométrico que se refiere a triángulos equiláteros. Según el teorema, si se toma el centro de cada uno de los nuevos triángulos formados y se los une, el resultado será siempre otro triángulo equilátero.
En el contexto de la batalla de Austerlitz, Napoleón podría haber aplicado este principio geométrico para determinar la disposición óptima de sus tropas y maximizar su eficacia táctica en el campo de batalla. Para ello, habría tenido que hacer cálculos precisos y estimaciones basadas en la topografía del terreno y la posición del enemigo.

Además del Teorema de Napoleón, también se habla del Problema de Napoleón, un famoso problema de construcción con compás en geometría euclídea. Este problema, que consiste en dividir un círculo en cuatro arcos iguales empleando solo un compás, podría haber tenido aplicaciones en la estrategia militar de Napoleón, permitiéndole dividir eficientemente sus fuerzas en el campo de batalla.
El enfoque matemático tiene ventajas significativas en la estrategia militar, como lo ejemplifica el caso de la batalla de Austerlitz con Napoleón.
- Precisión: La matemática garantiza precisión en las estimaciones y cálculos, un aspecto crucial en la planificación y ejecución de estrategias militares.
- Predicción: Permite anticipar y planificar movimientos en función del comportamiento del enemigo, terreno o condiciones de batalla.
- Optimización de recursos: Asegura la eficiente distribución y utilización de las tropas, maximizando su potencial en el campo de batalla.
No obstante, también presenta limitaciones:
- Incumplimiento de supuestos: Los modelos matemáticos se basan en supuestos que pueden no corresponder con la realidad del campo de batalla.
- Dependencia de datos precisos: Los cálculos requieren datos precisos y actualizados, que a veces pueden ser difíciles de obtener en una situación de guerra.
- Incertidumbre e imprevisibilidad: La guerra es un escenario intrigante y dinámico que puede cambiar rápidamente, desafiando los pronósticos y estrategias basadas en cálculos matemáticos.
Qué es real y qué es ficción sobre Napoleón en Austerlitz
En la representación de Napoleón en Austerlitz, es necesario distinguir entre hechos y ficciones. En términos generales, es cierto que Napoleón logró una victoria espectacular en la batalla de Austerlitz, derrotando a las fuerzas combinadas de Austria y Rusia a pesar de estar en desventaja numérica. Sin embargo, la representación cinematográfica puede exagerar o inventar ciertos aspectos para lograr un mayor impacto dramático. Un ejemplo es la representación de un lago congelado en la batalla de Austerlitz, descrita en algunas películas. Según los informes históricos, la batalla ocurrió cerca de pequeñas lagunas, no de un gran lago helado. Además, la táctica de Napoleón fue diferente a lo que se muestra en algunas representaciones cinematográficas.

Además de su destreza militar, Napoleón Bonaparte también se destacó en el campo de las matemáticas. Aunque no se conservan registros directos de sus conocimientos matemáticos, varias fuentes sugieren que tenía una gran habilidad para los cálculos y las estimaciones.
Se cree que su interés en las matemáticas se despertó durante su formación en la École Militaire en París, donde los futuros oficiales militares recibían una rigurosa educación en matemáticas aplicadas para ayudarles en tareas como la artillería y la ingeniería.
En el contexto de la batalla de Austerlitz, es plausible que Bonaparte utilizara su conocimiento matemático para perfeccionar su estrategia. Por ejemplo, podría haber empleado principios geométricos para optimizar la disposición de sus tropas, o cálculos de probabilidad para evaluar los posibles resultados de sus decisiones tácticas.

Además, el legendario "Teorema de Napoleón" lleva su nombre, aunque no hay evidencia concreta de que él lo haya descubierto. Sin embargo, este teorema, que describe una propiedad sorprendente de los triángulos equiláteros, es un ejemplo de cómo las matemáticas pueden proporcionar soluciones inesperadas y elegantes a los problemas, algo que sin duda habría atraído a la mente analítica de Napoleón.
En resumen, aunque no existe una "huella" matemática específica de Bonaparte en Austerlitz, su formación y su inclinación por las matemáticas ciertamente jugaron un papel en su enfoque estratégico y su éxito en el campo de batalla. (Con IA)











